Formules mathématiques lycée
|
Identités remarquables (a+b)²=a²+2ab+b² (a-b)²=a²-2ab+b² (a+b)(a-b)=a²-b² (a+b)³=a³+3a²b+3ab²+b³ (a-b)³=a³-3a²b+3ab²-b³ a³+b³=(a+b)(a²-ab+b²) a³-b³=(a-b)(a²+ab+b²) |
Equation du second degré Soient a, b et c trois nombres réels (a≠0) et Δ=b2 - 4ac. L'équation ax2 + bx + c=0 admet: - Lorsque Δ>0, deux solutions réelles x1=(-b-√Δ)/(2a) x2=(-b+√Δ)/(2a) - Lorsque Δ=0, une solution réelle x1=-b/(2a) - Lorsque Δ<0, aucune solution réelle. Si Δ>0, ax2 + bx + c = a(x-x1)(x-x2) Si Δ=0, ax2 + bx + c = a(x-x1)2 |
||||
| Fonctions logarithme et exponentielle e0=1 ea+b=eaeb ea-b=(ea)/(eb) (ea)b=eab lne=1 ln1=0 lnab=lna+lnb ln(a/b)=lna-lnb ax=exlna lnax=xlna y=ex⇔x=lny |
Dérivées et primitives des fonctions usuelles
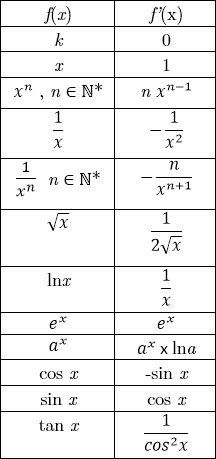
|
Opérations et application des dérivées
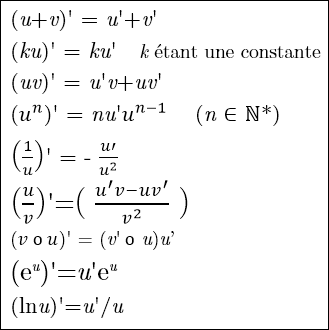
Equation de la tangente à la courbe Cf en A(a; f(a)) : y = f '(a)(x - a)+ f(a) |
|||
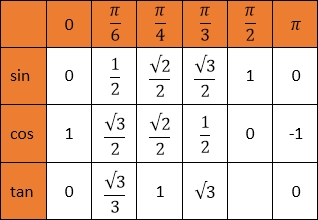
Trigonométrie
|
|||||
Limites usuelles de fonctions
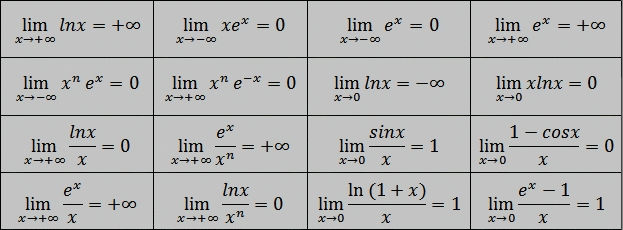
Accroissements
Pour une fonction f définie sur un intervalle [a,b] (où a < b) :
L'accroissement moyen de f sur [a,b] est :
Si f(a) ≠ 0, l'accroissement relatif de f sur [a,b] est :
L'accroissement moyen de f sur [a,b] est :
$$f(b)-f(a)\over b-a$$
Si f(a) ≠ 0, l'accroissement relatif de f sur [a,b] est :
$$f(b)-f(a)\over f(a)$$
Suites arithmétiques, suites géométriques
Suite arithmétique de premier terme u0 ∈ ℝ et de raison a ∈ ℝ
Pour tout n ∈ ℕ,
Suite géométrique de premier terme u0 ∈ ℝ et de raison b ∈ ℝ*
Somme de termes :
Si b ≠ 1 alors :
Pour tout n ∈ ℕ,
|
$$u_{n+1}=u_n+a$$
|
$$u_n=u_0+na$$
|
Suite géométrique de premier terme u0 ∈ ℝ et de raison b ∈ ℝ*
|
$$u_{n+1}=bu_n$$
|
$$u_n=u_0b^n$$
|
Somme de termes :
$$1+2+...+n= \frac{n(n+1)}{2}$$
Si b ≠ 1 alors :
$$1+b+b^2+...+b^n= \frac{1-b^{n+1}}{1-b}$$