Dans le repère hortonormal (O;u;v) le point M(x,y), où (x,y) ∈ ℝ², a pour affixe z.




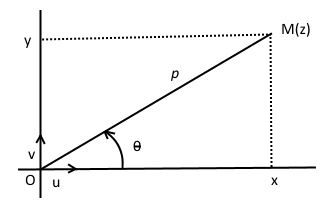
z a pour forme algébrique x+iy.
Partie réelle de z : Re(z)=x
Partie imaginaire de z : Im(z)=y
Conjugué de z : z̄=x-iy

Module de z :

$$|z| = \sqrt{zz̄} = \sqrt{x^2+y^2}$$

si z ≠ 0,
z a pour forme trigonométrique : z = ρ(cosθ + isinθ)
z a pour forme exponentielle : z = ρe^iθ
Module de z : |z| = ρ
Argument de z : arg z = θ[2π]
Conjugué de z : z = ρe^-iθ


Propriétés des modules
Pour tout z ∈ ℂ, |z̄| = |z|

Pour tout z ∈ ℂ* ,

$$|1/z| = 1/|z|$$

Pour tout z ∈ ℂ et z' ∈ ℂ, |zz'| = |z||z'|

Si A et B ont pour affixes respectives zA et zB alors

$$\overrightarrow{AB}$$

a pour affixe zB - zA et AB = |zB - zA|

Propriétés des arguments
Pour tout z ∈ ℂ* et z' ∈ ℂ* ,
arg(zz') = arg(z) + arg(z') [2π]
arg(^z⁄_z') = arg(z) - arg(z') [2π]

Caractérisation complexe de transformations

$$M(z) \rightarrow M'(z')$$

Translation de vecteur

$$\overrightarrow{u}$$

d'affixe t, t ∈ ℂ : z' = z + t

Homotéthie de centre Ω d'affixe ω, ω ∈ ℂ et de rapport k ∈ ℝ* : z' - ω = k(z - ω)
Rotation de centre Ω d'affixe ω, ω ∈ ℂ, et d'angle de mesure θ ∈ ℝ : z' - ω = e^iθ(z - ω)